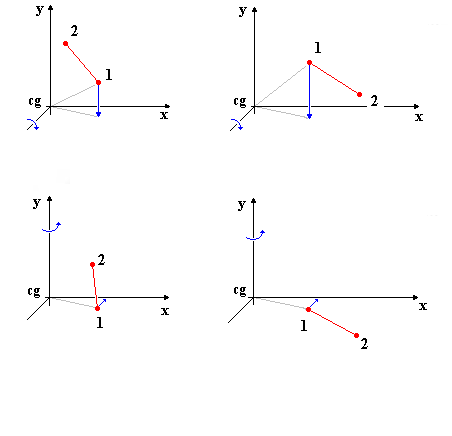
Εικόνα Α. Περιστροφές για Tαύτιση του Πρώτου Ατόμου
Η διαδικασία πρόβλεψης της τριτοταγούς δομής ομόλογων πρωτεϊνών στηρίζεται αποκλειστικά στο γεγονός ότι υπάρχουν μεγάλα ποσοστά ομοιότητας μεταξύ των τριτοταγών περιοχών τους. Αυτό σημαίνει ότι αν κάποιος παρατηρήσει τη στερεοδιάταξη των μορίων τους στο χώρο θα διαπιστώσει ότι μεγάλα τμήματα των δομών μοιάζουν ως προς τη γεωμετρία τους. Αν επιπλέον μετακινήσουμε τα μόρια ώστε να συμπέσουν οι όμοιες (γεωμετρικά) περιοχές τους θα δούμε ότι τα μόρια σε ένα μεγάλο ποσοστό ταυτίζονται. Αυτό είναι ουσιαστικά το χαρακτηριστικό που τους δίνει κοινές φυσικοχημικές ιδιότητες (που συνεπάγεται παρόμοια λειτουργικότητα) και τα κατατάσσει στην ίδια οικογένεια πρωτεϊνών.
Το χαρακτηριστικό της ταύτισης ολόκληρων δομικών περιοχών θα αξιοποιήσουμε στη διαδικασία σύνθεσης της δομής της άγνωστης πρωτεΐνης που θα μελετάμε. Στηριζόμαστε δηλαδή στην υπόθεση ότι η άγνωστη πρωτεΐνη θα έχει μεγάλες ομοιότητες με τις υπόλοιπες πρωτεΐνες της οικογένειας της και κατά συνέπεια θα μπορούμε να προσαρμόσουμε τη γεωμετρία της πάνω στη γεωμετρία των υπολοίπων. Φυσικά αναφερόμαστε στα κοινά του (γεωμετρικά) τμήματα και όχι στο σύνολο των δομών τους.
Ο εντοπισμός των κοινών δομικών περιοχών θα οδηγήσει στο επόμενο βήμα που θα είναι η επιλογή κάποιων από αυτά για συναρμολόγηση του μοριακού προτύπου της άγνωστης δομής. Η επιλογή αυτή θα γίνει με βάση τη χημική σύσταση των τμημάτων της άγνωστης δομής που ταυτίζονται στο πρωτοταγές επίπεδο με τμήματα των κοινών τριτοταγών περιοχών. Είναι καθοριστικό λοιπόν να εντοπίσουμε σωστά τα κοινά τμήματα της τριτοταγούς δομής της οικογένειας των πρωτεϊνών που μελετάμε.
Ο εντοπισμός αυτός μπορεί να γίνει με χειρωνακτική (υπολογιστικά) μετακίνηση του ενός μορίου πάνω στο άλλο μέσα από μια διαδικασία περιστροφών και μεταφορών ή με τη χρήση κατάλληλου λογισμικού που θα το κάνει αυτόματα. Η πρώτη διαδικασία περιλαμβάνει επίπονες δοκιμές και σφάλματα χωρίς να εγγυάται την ιδανική ταύτιση των δομών. Η δεύτερη επιλογή είναι επιστημονικά πιο αποδεκτή λόγω της ακρίβειας των αποτελεσμάτων της και της θεωρητικής επιβεβαίωσης της μεθοδολογίας της.
Προσέγγιση με τη Μέθοδο των Ελαχίστων Τετραγώνων
Μετά την τελειοποίηση της ευθυγράμμισης των ακολουθιών στο πρωτοταγές επίπεδο θα πρέπει να δούμε την "ευθυγράμμισή" τους (ταύτιση των δομών τους) στο χώρο. Αυτή είναι βασικά η κυρίαρχη μορφή ταύτισης που κατατάσσει τις πρωτεΐνες σε ομόλογες οικογένειες. Μέσα από αυτό το είδος ευθυγράμμισης θα δούμε τις πραγματικές ομοιότητες των πρωτεϊνών και τον κοινό τρόπο δράσης τους. Πολλές από τις ομοιότητες που εντοπίσαμε στις ευθυγραμμίσεις των αμινοξικών τους ακολουθιών θα διατηρούνται και στο τριτοταγές επίπεδο ενώ κάποιες άλλες θα εξαφανίζονται. Παρόμοια θα δούμε τμήματα των ακολουθιών που δεν εμφάνιζαν ουσιαστικές ομοιότητες στο πρωτοταγές επίπεδο, να παρουσιάζουν δομικές ομοιότητες στο τριτοταγές.
Γενικά είναι σίγουρο ότι η ταύτιση των τριτοταγών δομών των ομόλογων πρωτεϊνών, για τις οποίες διαθέτουμε κρυσταλλογραφικά δεδομένα, θα προβάλει όσο πιο έντονα γίνεται τα κοινά τους χαρακτηριστικά και το βαθμό συγγένειας τους. Τα μοριακά πρότυπα που παράγονται μετά από τη διαδικασία ταύτισης, θα μας δώσουν τις πληροφορίες που χρειαζόμαστε για την τελική επιλογή των τμημάτων που θα συνθέσουν την άγνωστη (κρυσταλλογραφικά) πρωτεΐνη που μελετάμε.
Για την ταύτιση των τριτοταγών δομών χρησιμοποιήθηκε η μέθοδος των ελαχίστων τετραγώνων που δοκιμάζοντας περιστροφές και μεταφορές των μορίων σε σχέση με το πρώτο από αυτά, καταλήγει στην ιδανική προσέγγιση τους. Η μέθοδος χρησιμοποιεί τις συντεταγμένες των ατόμων των πρωτεϊνών όπως εμφανίζονται στα αρχεία των κρυσταλλοδομών τους. Μετά την επεξεργασία το αντίστοιχο λογισμικό παράγει αντίστοιχα αρχεία με τις συντεταγμένες τροποποιημένες ώστε να αντιστοιχούν στις ιδανικές προσεγγίσεις.
Ερχόμαστε τώρα στη διαδικασία ταύτισης των διαθέσιμων τριτοταγών δομών. Σε πρώτη φάση θα πρέπει να εντοπίσουμε τα κατάλοιπα εκείνα τα οποία υπάρχουν σε χαρακτηριστικές θέσεις σε όλες τις πρωτεΐνες και που πιστεύουμε ότι παίζουν ουσιαστικό ρόλο στην τελική δομή των μορίων. Τα κατάλοιπα αυτά θα πρέπει κατά προτίμηση να βρίσκονται σε συνεχόμενα τμήματα των ακολουθιών και να εμφανίζονται σε όλες τις ομόλογες πρωτεΐνες. Καλό είναι να διαθέτουν ένα επιπλέον χαρακτηριστικό όπως η συμμετοχή τους στο ενεργό κέντρο ή σε κάποιο χαρακτηριστικό δεσμό όπως οι κυστεΐνες. Ένα ίσως από τα πιο χαρακτηριστικά κατάλοιπα που συνιστάται να χρησιμοποιείται σαν σημείο αναφοράς είναι οι προλίνες. Αυτό οφείλεται στην ιδιομορφία της δομής τους, που επιφέρει συνήθως κάμψεις της αμινοξικής αλυσίδας απαραίτητες για τη λειτουργική δόμηση των πρωτεϊνικών μορίων.
Στις περιπτώσεις που έχουμε στη διάθεση μας δεδομένα δευτεροταγών δομών συνιστάται να κάνουμε την επιλογή καταλοίπων από τμήματα των δομών αυτών που ταυτίζονται μεταξύ τους. Αυτό θα ενισχύσει τα αποτελέσματα ταύτισης λόγω της ισχυρής τάσης διατήρησης αυτών των τμημάτων.
Με κριτήρια που εξαρτώνται γενικά από το χρήστη θα πρέπει να επιλεγούν κάποια κατάλοιπα σαν σημεία αναφοράς για το κριτήριο ταύτισης των τριτοταγών δομών. Ιδανικά το πλήθος των καταλοίπων που επιλέγονται για αυτό το σκοπό θα πρέπει να ξεπερνάει τα τρία. Αυτό οφείλεται στο ελάχιστο πλήθος μεταβλητών που είναι απαραίτητες για τον καθορισμό της θέσης και του προσανατολισμού ενός στερεού σώματος. Όσο μεγαλύτερο είναι το πλήθος τόσο καλύτερο θα είναι το αποτέλεσμα της προσέγγισης των δομών. Ταυτόχρονα θα πρέπει να αποφεύγεται η χρήση πολύ μεγάλου πλήθους καταλοίπων αναφοράς, τουλάχιστον σε πρώτη φάση, λόγω της αρχικής άγνοιας της λεπτομερούς μορφολογίας των μορίων.
Στην πράξη επιχειρούμε πρώτα την ταύτιση των δομών με ένα πλήθος της τάξης των πέντε με οκτώ καταλοίπων αναφοράς και στη συνέχεια αν το αποτέλεσμα είναι ικανοποιητικό προχωράμε στην επιλογή περισσότερων, με βάση πάντα τα αποτελέσματα της αρχικής ταύτισης. Στις περιπτώσεις που θέλει κανείς να ταυτίσει τις δομές χωρίς κανένα κατάλοιπο αναφοράς ή με λιγότερα από τέσσερα τότε η διαδικασία ευθυγράμμισης ακολουθεί μια μεθοδολογία δοκιμής και σφάλματος με πολλούς συνδυασμούς καταλοίπων μέχρι να καταλήξει σε ένα ικανοποιητικό αποτέλεσμα. Αυτό σημαίνει ότι ο χρόνος εκτέλεσης του προγράμματος για την παραγωγή ικανοποιητικών αποτελεσμάτων θα αυξηθεί υπερβολικά. Ένας άλλος λόγος που την κάνει απαραίτητη σε ένα πακέτο λογισμικού είναι ο αυτοματισμός που παρέχει που γενικά είναι απαραίτητος για χρήστες που δεν είναι ειδικευμένοι και εξοικειωμένοι με παρόμοιες διαδικασίες. Η μεθοδολογία προσέγγισης σ' αυτή την περίπτωση θα παρουσιαστεί σε ξεχωριστή παράγραφο λόγω του ενδιαφέροντος που παρουσιάζει για χρήση στα αρχικά τουλάχιστον στάδια μελέτης.
Σε όλη τη διαδικασία ταύτισης τα κατάλοιπα αντιπροσωπεύονται, τουλάχιστον στην παρούσα εργασία, με τις συντεταγμένες των Ca ανθράκων τους. Πιθανόν κάποιος χρήστης να επιθυμούσε κάποια άλλα άτομα, αλλά στην πλειοψηφία των περιπτώσεων οι Ca άνθρακες είναι απόλυτα ικανοποιητικοί. Τουλάχιστον από τις περιπτώσεις που είδαμε μέσα από την παρούσα εργασία βρήκαμε ότι η επιλογή αυτών των ατόμων ήταν η πιο απλή και ασφαλής λύση.
Η ταύτιση των τριτοταγών δομών ανάγεται, όπως είπαμε και προηγουμένως, σε ταύτιση στερεών σωμάτων. Η διαδικασία που υιοθετήσαμε γι' αυτό το σκοπό περιλαμβάνει την εφαρμογή του κριτηρίου των ελαχίστων τετραγώνων με κατάλληλη επιλογή γωνιών στροφών που εγγυάται τη μεταφορά του ενός στερεού (πρωτεΐνη) στο άλλο. Η επιλογή αυτής της μεθοδολογίας έγινε με βάση την αξιοπιστία της και τη μεγάλη δημοτικότητά της στις μαθηματικές μεθόδους της μοριακής βιολογίας και των επιστημών γενικότερα. Αναλυτική περιγραφή των μεταβλητών που χρησιμοποιήσαμε και του κριτηρίου των ελαχίστων γίνεται στο Παράρτημα Α. Εκεί αναπτύσσονται όλες οι εξισώσεις που χρησιμοποιούνται για την περιγραφή των πρωτεϊνικών μακρομορίων σαν στερεά ανελαστικά σώματα.
Για την αποφυγή των προβλημάτων αναλυτικής επίλυσης και αριθμητικών μεθόδων που συνεπάγεται η επίλυση του συστήματος των μερικών παραγώγων (Παράρτημα Α) όπως αυτές προκύπτουν από την εφαρμογή του κριτηρίου των ελαχίστων τετραγώνων, καταφύγαμε (για τις ανάγκες της παρούσας εργασίας) στην επιλογή μιας πιο απλής και συνηθισμένης λύσης. Στηριχτήκαμε πρωταρχικά στο γεγονός ότι όλες σχεδόν τις φορές ο χρήστης προτιμάει να επιλέξει κάποια ζεύγη ατόμων Ca (καταλοίπων στην ουσία) που φαίνεται από τις ευθυγραμμίσεις ότι διατηρούνται. Η Lsq_Fit βρίσκει σε πρώτη φάση το γεωμετρικό κέντρο αυτών των καταλοίπων και μεταφέρει όλα τα γεωμετρικά κέντρα στην αρχή των αξόνων. Η διαδικασία αυτή τακτοποιεί ουσιαστικά τις μεταφορικές κινήσεις των μορίων κατά το πλησίασμα της μιας δομής στην άλλη.
Στη συνέχεια η μέθοδος επιχειρεί μια πρώτη
ταύτιση ένα προς ένα χρησιμοποιώντας τα δύο πρώτα "ζεύγη" ατόμων. Η διαδικασία
είναι σχετικά απλή και περιλαμβάνει, όπως φαίνεται και στην εικόνα Α, αρχικά
περιστροφή των μορίων ώστε να τοποθετηθούν τα πρώτα άτομα πάνω στο θετικό
ημιάξονα του άξονα x'x. Με μπλε βέλη
φαίνονται οι περιστροφές και οι μετατοπίσεις που γίνονται. Στο σχήμα έχουμε
τη διαδικασία ταύτισης δύο συνόλων ατόμων, δύο διαφορετικών μορίων, αριστερά
και δεξιά. Αρχικά το πρώτο άτομο μεταφέρεται στο επίπεδο xz
με περιστροφή γύρω από τον άξονα z'z
και στη συνέχεια μεταφέρεται στον άξονα x'x
με περιστροφή γύρω από τον y'y.
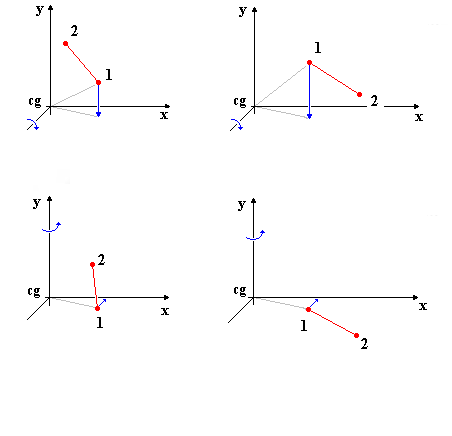
Εικόνα Α. Περιστροφές
για Tαύτιση του Πρώτου Ατόμου
Στην συνέχεια τα μόρια περιστρέφονται ώστε τα δεύτερα άτομα να συμπέσουν με το επίπεδο xy και προς την πλευρά του θετικού ημιάξονα του y'y. Στην εικόνα Β βλέπουμε τις αντίστοιχες μετακινήσεις για το δεξιό και αριστερό μόριο. Θα πρέπει να παρατηρήσουμε ότι η μεταφορά τους στο χώρο του θετικού ημιάξονα του y'y μπορεί να απαιτήσει μία επιπλέον περιστροφή στην περίπτωση που η προηγούμενη ενέργεια μεταφέρει το δεύτερο άτομο στο χώρο του αρνητικού ημιάξονα του y'y. Αυτό συνέβη και στην περίπτωση του δεξιού μορίου. Με τον τρόπο αυτό έχουμε εξασφαλίσει ένα μονοσήμαντο προσανατολισμό όλων των μορίων και πετύχαμε μια πρώτη ταύτιση των δομών τους.
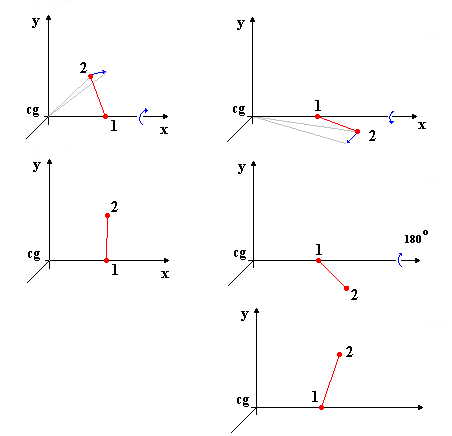
Εικόνα Β Περιστροφές για Ταύτιση του Δεύτερου Ατόμου
Η αρχική αυτή ταύτιση αντιπροσωπεύει μια πάρα πολύ καλή αρχική εκτίμηση των προσανατολισμών των μορίων. Αυτό φάνηκε από τις διάφορες δοκιμές που έγιναν για την εκτίμηση της αξιοπιστίας της διαδικασίας καθώς και από τα τελικά αποτελέσματα που θα αναφέρουμε στο τρίτο τμήμα (εφαρμογές) της παρούσας εργασίας. Καθοριστικό ρόλο προφανώς παίζει η επιλογή των τριών πρώτων "ζευγών" κυρίως στο χρόνο εκτέλεσης του προγράμματος και όχι ιδιαίτερα στην ποιότητα των αποτελεσμάτων που θα πάρουμε.
Στο επόμενο στάδιο επεξεργασίας η μέθοδος σαρώνει το χώρο των δυνατών προσανατολισμών και θέσεων των μορίων ώστε να εντοπίσει την περιοχή που το κριτήριο που χρησιμοποιούμε θα παρουσιάζει ελάχιστο. Η σάρωση γίνεται με τη δημιουργία ενός "πλέγματος" που καλύπτει το χώρο των δυνατών τιμών των μεταβλητών (Εικόνα Γ). Με την κατάλληλη επιλογή των διαστάσεων των κυψελίδων του πλέγματος μπορούμε να έχουμε μια πλήρη κάλυψη του χώρου. Ταυτόχρονα η επιλογή των διαστάσεων (που είναι ουσιαστικά το βήμα με το οποίο καλύπτεται ο χώρος) θα πρέπει να έχει σχετικά μεγάλη τιμή ώστε η διαδικασία να εντοπίζει το ελάχιστο σε πρακτικά σύντομο χρονικό διάστημα. Στην πράξη επιλέγουμε ένα βήμα αρκετά μεγάλο αλλά ταυτόχρονα ικανοποιητικό για τον προσεγγιστικό εντοπισμό του ελάχιστου. Στην συνέχεια μικραίνουμε τις διαστάσεις του πλέγματος στην περιοχή που εντοπίσαμε και προσεγγίζουμε καλύτερα το ελάχιστο. Η διαδικασία αυτή συνεχίζεται μέχρις ότου η προσέγγιση πλησιάσει το πειραματικά αποδεκτό σφάλμα των κρυσταλλογραφικών δεδομένων που έχουμε.
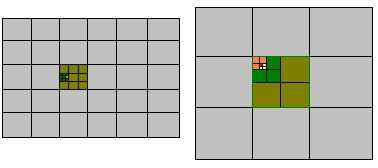
Εικόνα Γ Δυδιάστατο πλέγμα σάρωσης
Στην περίπτωση της ταύτισης των τριτοταγών δομών των πρωτεϊνών η παραπάνω διαδικασία περιλαμβάνει αρχικά περιστροφές των μορίων από τις -90ο στις +90ο για κάθε άξονα του τρισορθογώνιου συστήματος, με ένα αρχικό βήμα 30ο. Σε κάθε θέση το πρόγραμμα υπολογίζει την ιδανική μεταφορά (για κάθε άξονα) που δίνεται από τις σχέσεις :
![]() ,
, ![]() ,
, ![]()
Με υπολογισμό του κριτηρίου που χρησιμοποιούμε εντοπίζει τις τιμές στροφής και μεταφοράς που έχουμε ελάχιστο και στη συνέχεια σαρώνει αυτή την υποπεριοχή από τις -30ο στις +30ο με βήμα τις 10 μοίρες και αντίστοιχα από +3Α σε -3Α με βήμα 1Α για τις μεταφορές. Η διαδικασία αυτή επαναλαμβάνεται μέχρι τελικά να έχουμε ένα βήμα μικρότερο της μίας μοίρας για τις περιστροφές και 0.2Α για τις μεταφορές, οπότε και η περιοχή με το ελάχιστο άθροισμα επιλέγεται σαν η καλύτερη.
Από τις τιμές των γωνιών που αναφέραμε
φαίνεται ότι το βήμα είναι πάντοτε το ένα τρίτο των τιμών εύρους των γωνιών
στροφής που χρησιμοποιούμε για τον ορισμό της κάθε υποπεριοχής με
ανάλογη σχέση και τα μεγέθη των μεταφορικών κινήσεων. Οι τιμές αυτές επιλέγηκαν
μετά από μελέτη της διαδικασίας σαν οι πιο ιδανικές για την ταχύτερη κάλυψη
του χώρου. Στην πραγματικότητα η ιδανικότερη τιμή της αρχικής γωνίας είναι
οι 40o και των μετατοπίσεων
τα 3Α για το σύνολο των ταυτίσεων που μελετήσαμε. Αυτό ενισχύει την επιτυχία
της διαδικασίας δεδομένου ότι οι πρώτες ταυτίσεις βρίσκονται αρκετά κοντά
στις ιδανικές. Η αρχική τιμή των 90ο για τις στροφές και των
9Α συνιστάται για την κάλυψη και των πιο σπάνιων περιπτώσεων όταν η επιλογή
των "ζευγών" αναφοράς είναι ατυχής.